L'Occhio infinito di Galileo - Apollonio di Perga e gli epicicli

Malgrado si eseguissero misurazioni eccezionali e si avessero intuizioni geniali, va ricordato che il pensiero dominante, di tipo filosofico-religioso, seguiva le indicazioni di Platone e dei pitagorici che vedevano l’universo come una successione di sfere cristalline, quindi solide, che trasportavano in successione nei loro movimenti attorno alla Terra, naturalmente immobile al centro del cosmo, la Luna, il Sole, Mercurio, Venere, Marte, Giove, Saturno e da ultimo la sfera delle stelle fisse. Soprattutto erano assolutamente indiscutibili gli assiomi della circolarità dei moti di tutti gli astri (il cerchio era la figura geometrica che maggiormente racchiudeva i caratteri della perfezione) e della uniformità nel percorrerli. Dove Platone proponeva innovazioni rispetto a Pitagora era nell’esortare gli astronomi a escogitare rigorosi metodi matematici che avrebbero permesso di spiegare le irregolarità (stazionamenti, moti retrogradi e apparenti variazioni di velocità) che venivano riscontrate nei moti planetari, salvando i fenomeni, cioè preservando i due assiomi pitagorici di cui sopra. Ricordiamo infatti che il moto apparente dei pianeti è piuttosto complesso, presentando traiettorie che formano “cappi” e che variano di velocità. Tutte cose che NON potevano essere spiegate con il semplice moto attorno alla Terra.

Il tipico moto apparente di un pianeta. Si nota il “cappio”, il cambiamento di direzione e la variazione di velocità.

Partendo quindi da idee errate, la grande capacità razionale e matematica dei greci riuscì a trovare modelli che spiegassero le anomalie riscontrate, in modo da non collidere con i principi fondamentali. Una grande fatica inutile, se vogliamo, ma una prova straordinaria delle applicazioni geometriche e matematiche, che porteranno alla fine al meraviglioso, anche se completamente sbagliato, modello tolemaico.

Apolonnio di Perga fu forse il primo a dare una versione scientifica alle incongruenze che apparivano nel modello pitagorico e di Platone. Egli visse dal 262 al 190 a.C. circa ed era noto come “il grande geometra”. Ebbe una grande influenza sullo sviluppo della matematica, specialmente per la sua opera più famosa, le coniche, in cui introdusse termini matematici quali ellisse, parabola, iperbole, che continuano ad essere usati.

Come già detto, fin dai tempi più antichi si erano osservate delle irregolarità nei movimenti del Sole e dei pianeti che non potevano spiegarsi con il consacrato moto angolare circolare ed uniforme. Secondo la terminologia introdotta dai matematici greci, si usavano le parole anomalia o anche inegualità per indicare qualsiasi irregolarità nei moti dei corpi celesti. La scoperta dell’anomalia solare risale talmente indietro nel tempo che è in pratica assurdo parlare di una sua scoperta. E’ però difficile pensare che uomini della levatura di Talete o di Anassimandro non abbiano meditato su di essa. Quanto ai Pitagorici, non ci sarebbe da meravigliarsi se, inorriditi, l’abbiano semplicemente rimossa. Quando l’evidenza delle osservazioni mostrò inequivocabilmente che anche per i pianeti si aveva un’anomalia, venne d’uso attribuirle il nome di anomalia zodiacale (velocità angolari diverse manifestate da Sole e pianeti in diverse parti dello zodiaco). Constatando poi che i pianeti manifestavano una anomalia tutta loro particolare (le retrogradazioni, ossia quegli strani “cappi” che descrivono nel cielo), a quest’altra irregolarità si attribuì il termine di seconda anomalia (e di conseguenza venne chiamata talvolta prima anomalia l’anomalia zodiacale). Per spiegare le anomalie, Apollonio introdusse in modo rigorosamente matematico le costruzioni geometriche degli epicicli e degli ex-centri.

Prima di procedere alla loro descrizione dobbiamo partire dall’epoca, invero molto remota, in cui si ebbe la cognizione della anomalia solare, che per gli Antichi era riscontrabile, in pratica, nelle differenti durate delle stagioni. Il primo che sembrerebbe aver eseguito una sua misura fu Callippo, nel 330 a.C. Ma le sue misurazioni furono alquanto imprecise (non disponeva di osservazioni attendibili di suoi predecessori). Non è da escludere comunque che anche prima di Ipparco (vedi nel seguito), che intorno al 130 a.C. eseguì la migliore determinazione di durata dell’anno e delle singole stagioni, i Greci avessero stabilito che le durate delle stagioni si potevano illustrare con uno schema come quello della figura che segue (la primavera è la più lunga, seguita dall’estate, poi dall’inverno e da ultimo dall’autunno, quindi ben differenti dalle durate delle stagioni odierne).

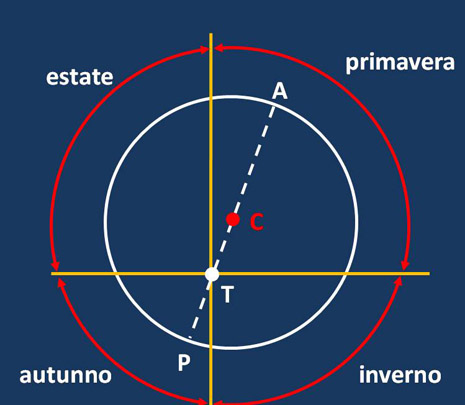
Per spiegare l’anomalia solare, ossia la durata diversa delle stagioni, fin da epoche remote si era forse pensato di porre il centro C dell’orbita solare fuori dalla Terra T (ex-centro). In tal modo si spiegava anche la velocità apparente del Sole più alta in P che non in A. Ciò era solo dovuto alla diversa distanza ed il moto circolare uniforme restava un assioma inviolato.
E quindi ancor prima di Apollonio, la diseguale durata delle stagioni avrebbe forse suggerito che l’anomalia solare poteva essere spiegata collocando il centro dell’orbita fuori del centro della Terra (ex-centro), come appare nella figura precedente. Ciò avrebbe spiegato come poteva avvenire che, pur descrivendo il Sole l’eclittica a velocità costante e con orbita circolare, dalla Terra apparisse che il tratto di orbita dalla parte più vicina era percorso a velocità maggiore di quella a cui era percorso il tratto dalla parte opposta.

Apollonio, da grande matematico, introdusse una costruzione geometrica particolare, dimostrando l’equivalenza con quella della figura precedente, continuando ad obbedire completamente ai canoni risalenti alla scuola pitagorica e consacrati dalla fisica aristotelica, che dovevano essere conservati. Questi canoni astronomici, già accennati precedentemente nella loro espressione esteriore, possedevano una intima valenza trascendente che andava ben oltre la loro semplice apparenza geometrica: erano i “fenomeni da salvare”, cioè: (1) l’orbita solare è un cerchio, (2) la Terra, essendo centro del cosmo, deve essere centro di questo cerchio e (3) la velocità del Sole su questo cerchio deve essere costante. Vediamo allora in dettaglio come sia riuscita in questa dimostrazione. Ci rendiamo perfettamente conto che questa trattazione potrebbe apparire un po’ ostica a molti lettori. Tuttavia, li invitiamo ad un piccolo sforzo, in quanto la nascita degli “epicicli” è fondamentale per il seguito delle teorie planetarie introdotte e seguite fino ai tempi di Galileo Galilei.

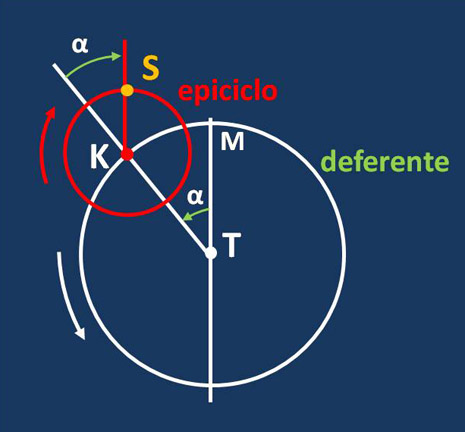
Il Sole si muove con un periodo di un anno su un cerchio perfetto con moto uniforme ed in senso orario, detto epiciclo, il cui centro K circola a sua volta, in senso antiorario, con moto uniforme e con lo stesso periodo di un anno, su un altro cerchio, detto deferente, che ha per centro la Terra.

Secondo Apollonio, dunque, il Sole circola con periodo di un anno, con moto uniforme e in senso orario su un cerchio, detto epiciclo, il cui centro circola a sua volta, in senso antiorario e con lo stesso periodo di un anno, su un altro cerchio, detto deferente, centrato nel centro della Terra. Vengono così conservati i principi base: cerchi perfetti, moti uniformi e Terra al centro.

In questa combinazione di movimenti il raggio dell’epiciclo del Sole si mantiene sempre orientato parallelamente ad una certa direzione. Ciò però è equivalente a dire che il Sole descrive un cerchio di raggio eguale al raggio del deferente, ma il cui centro è spostato fuori del centro della Terra (ex-centro) di una quantità pari al raggio dell’epiciclo solare. In definitiva quindi è come se il Sole circolasse su un cerchio (uguale al deferente) ma avente centro diverso dalla Terra. L’equivalenza è perfettamente dimostrata, come illustrato nella figura che segue.

La teoria geometrica degli epicicli e del deferente permetteva di ottenere lo stesso risultato di un orbita circolare del Sole attorno ad un punto C (ex-centro) non coincidente con la Terra.

Veramente un’operazione matematica e geometrica geniale, anche se del tutto … sbagliata. In modo analogo, anche se più complicato, Apollonio spiegava il moto dei pianeti interni ed esterni, dando ragione di molte anomalie. In realtà però molte cose non tornavano esattamente. Tuttavia, lo studioso, essendo soprattutto un matematico, non se ne curò più di tanto.

Resta comunque valido il fatto che la piattaforma matematica di Apollonio sarà quella che consentirà a Tolomeo di conseguire i suoi notevoli progressi astronomici. E’ quindi del tutto lecito accordare ad Apollonio un posto di assoluto rilievo.